Information: Technical Lecture

Transcript of Ralph Novak’s Lecture on Scale Length and
Tone to the 1995 G.A.L. Convention

From American Lutherie,
published quarterly by the Guild of American Luthiers.

When we choose the parameters for constructing an instrument on a tonal basis, such as woods, thicknesses, or bracing, for example, we may exercise what I call an intuitive familiarity with the tonal effects of our various choices on the finished instrument. I'd like us all to be able to exercise the same intuitive familiarity with regard to our scale length choices so that we can more precisely model our tonal goal.

One of the fascinating things about this craft is that there is not just one way of doing things. New methods, and even completely revolutionary ideas, are being injected into the craft continually, enhancing its refinement and growth. It is inspiring and stimulating to see a new approach that is also well executed. Results matter.

During today's instrument exhibition, besides checking out some fine work and great design ideas, I took an informal poll to see how different makers thought about scale length. Most builders shared the big picture of what they were looking at when they were building their guitars and how scale length fit into that picture. I got many different answers to my question:

• Some said they were looking specifically at size. A short scale was appropriate for a small instrument.
• Some said they were adhering to tradition. The type of instrument they were making had always used that scale.
• Some said tension, relative to either "feel" when played or structural stress.
• Some said tooling. They use commercially available jigs or the Ibex Fret Rule.
• Some said tone. They liked the sound of that scale length with their instrument design.

Scale Length

When we build an instrument, we pay critical attention to the components that go into it. We manipulate materials and structure for aesthetics, longevity, strength, and tone. Scale length fits directly into these considerations and may dictate some of the parameters. Scale length comes first because the harmonic content of the final tone produced by the instrument begins with the string. Factors such as structure and materials can only act as "filters" to tone; they can't add anything, they only modify input. Therefore, if the harmonic structure is not present in the string tone, it won't exist in the final tone. Woods, bracing, thickness, pickups, and electronics: these are controlling factors. The string is the originating factor, and therefore, parameters that control string harmonic output have utmost bearing on tone.

The familiar example might be the "Strat vs. Les Paul" comparison: as stock instruments they have distinctly different voices. We could put the Les Paul pickups in the Strat and vice-versa, then take the screws out of the Strat neck and glue it in, and break out the Les Paul neck and screw it back in. Voila! The Strat still maintains much of its clear, cutting quality, although a bit "fatter," and the Les Paul still has a round attack and mushy bass, although "thinner." We've discovered that the pickups and construction can't override the tonal effects of scale length. The upper partials present in the harmonic structure of the longer scale Strat string tone give it a cutting clarity that distinguish it from the sweet, round, lower partials that dominate the shorter scale Les Paul string tone.

The tone of an instrument originates with the string, and the primary factor that controls string tone (except for defective strings) is scale length. And since scale length affects tension and structural stresses, it may control other factors of our design, such as dimension and material choices. Therefore, when we get that vision of our ideal tone dancing in our heads, we must begin by selecting the scale length that complements our tonal recipe.

We probably are all familiar with the three basic laws of string vibration, if not exactly, then intuitively. These laws were described by Pythagoras, and set down by the French mathematician, Mersenne, in 1636.

1. If the mass and tension stay the same and the length is changed, the pitch changes. This change in pitch is proportional to the length. For example, halving the string length doubles the frequency (raises the pitch one octave).
2. If the mass and length stay the same, a change in tension results in a change in pitch proportional to the square root of the tension. For example, four times the tension results in a pitch change of one octave (double the frequency).
3. If the length and tension are constant, the change in pitch is inversely proportional to the square root of the mass of the string. For example, four times the mass results in a pitch change of one octave (half the frequency).

Theory is fine, but we're building guitars. Let's confine ourselves to concrete reality. Certain string gauges (mass) are commonly used, certain tunings (tension) are commonly used, and certain scale lengths are practical and common.

Tension, Gauge & Length

I'd like to share my way of understanding how string tension, string gauge, and string length relate to each other. In Fig. 1 scale length becomes the fulcrum of a balance between string gauge (mass) and string tension (tuning). If we move toward the left (shorter scale length) to keep the gauge in balance with the tension, we must increase the gauge or decrease the tension. The opposite is true if we increase the scale length. Given the technology of string making and the availability of commonly gauged string sets, we really don't have a very wide range of choices for a given scale length and tuning, so it is relatively easy to develop an intuitive familiarity with the harmonic voices of different scale lengths for the particular instruments we make.
An example of how we can use this relationship in practical terms might be the case of a guitarist who likes to use the dropped D tuning, where the low E string is lowered in pitch one whole step.

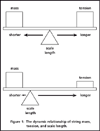Fig 1: The dynamic relationship of string mass, tension, and scale length.

If the player is using a Martin D 18 with light gauge strings, he may possibly get an acceptable tone from the slackened .054 gauge string. The experienced player knows that a bit heavier string sounds better when tuned down this way. The increased tension of the heavier string improves brightness and definition, and the increased mass improves volume. So, the player reasons, if the .058 sounds good, how about a .065? Here's where we cross the line: the stiffness of a .065 string at the D18 scale length is too great. The string can't divide up into enough harmonic nodes to render a pleasing tone, or a precise, sustained pitch. Yet, that same string on a 34" scale bass sounds great. One of the laws of string vibration relates to stiffness: stiffness implies a certain limit to the number of divisions a vibrating string can accommodate.

At this point, I'd like us to turn our attention to solidbody electric guitars, although this may stimulate an allergic reaction in some of you. The solidbody electric guitar is a nearly ideal tool to examine scale length tone because it can display, dramatically, the tonal effects of different scale lengths. Its solid construction introduces fewer resonances to color the tone. Also, it doesn't dissipate energy from the string as quickly as a diaphragm, so the voice of the string is clearer and more sustained. Modern electric guitar players and builders generally recognize two commonly used scale lengths: the "Gibson" scale, at 24 5/8 " (not 24 3/4") and the "Fender" scale at 25 1/2". Interestingly, Fender used the scale that Epiphone used at the time for most of its models. The demands of archtop players for instruments with more power to play ensemble with a band, and the top end to cut through, led the Epiphone company to adopt the longer scale. Gibson actually makes instruments with several different scale lengths, some of their archtop models also having a 25 1/2 " scale length. Most solidbody players, however, will know the 24 5/8" scale length because Gibson uses it for almost all of their solidbody line. There is an emerging awareness of the subtle differences in a third scale length, the 25 " scale, as used by Danelectro (Silvertone) and Paul Reed Smith, among others. Players seem to recognize it as a distinctive tone, not a compromise between "Gibson" and "Fender."

Spectrum Analysis

The following spectrum analyses charts were made with a monochord. This solidbody instrument has a single string, a fixed bridge with a piezo transducer under the saddle, and a moveable nut. Further, I made a mechanical picker to consistently pluck the string, as altering picking intensity alters harmonic content. It was also adjustable to pluck at a determined fraction of the string length for each scale length.

Principal to these tests was Bill Bartolini, who put considerable time and energy into this project. Most of you know Bill's great guitar and bass pickups, but few of you know of his passion for guitar making or his extensive research into classical guitar construction. "Experimental Studies of the Acoustics of Classic and Flamenco Guitars," by W. Bartolini and P.A. Bartolini, published in the Journal of Guitar Acoustics, is a landmark work and I recommend it as required reading. Bill's interest in all aspects of guitar design is what allowed me to tempt him with this project, coinciding neatly with his acquisition of some new computerized test equipment.

A program that analyses the harmonic content of a tone over a specified time period captures a sample and "transforms" the sound into a spectral analysis of the harmonic components and their relative intensity. The graphic output is called a Fourier transform, and is not a waveform such as you might see with an oscilloscope. This is not attack, sustain, and decay. It is a graphic analysis of the harmonic content of a tone with the "spikes" representing the most intense frequencies. Attack, sustain, and decay do figure in some aspects of scale length tone, but we're focusing on harmonic content. I don't mean to imply that this is the final word on the subject. While we did everything possible to maintain consistency and accuracy, these are only results that we got under these conditions and with this equipment. I do, however, believe that the general conclusions obtained by these tests are reasonably accurate and give us some guidelines that we can use.

In addition, before I show you the first transform, I must invoke Helmholtz, who tells us that no two sounds of different quality can correspond to the same mode of vibration; many different modes of vibration can give rise to a sound of only one quality. What this means relative to our spectrum analysis is that the harmonic content and magnitudes that comprise a tone are unique to that tone. It can't sound the same and look different, or look the same and sound different.

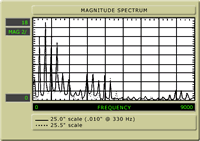
Fig. 2 shows a .010 gauge high E string at 330Hz. The scale along the bottom represents the frequencies from 0 to 5KHz, with each division representing .500Hz. The vertical scale represents magnitude, or intensity, measured in millivolts. It is sort of an arbitrary number for our purposes, but it gives us a good relative comparison. Observe that there are peaks of intensity (spikes) that correspond to the frequencies 330Hz, 660Hz, 990Hz, and 1320Hz, and at a lower intensity, 1650Hz, 1980Hz, etc. These correspond to the "textbook" harmonic series attributed to a vibrating string.

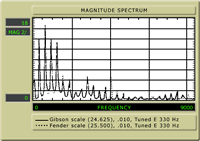
Fig. 2

The first peak, at 330Hz, is the fundamental. Then, the first partial (or harmonic) which is the second peak at 660Hz. Here the string is "dividing" in half (one node in the middle) and sounding an octave higher. The second harmonic is the third peak, at 990Hz, which shows the string "dividing" into thirds (two nodes) and sounding an octave and a fifth above the fundamental. The third harmonic is the fourth peak, at 1320Hz, with three nodes, and sounding two octaves above the fundamental (four times the frequency). We can continue, but I think we're all up to speed on this.

Vibrating String

Did someone say textbook? While we're in an academic frame of mind, let's recall some of the principles of the vibrating string and see how they apply to our transform. One point we've mentioned already is that the louder intensity harmonics contribute more of their voice to the tone. Relative to this, it is also generally accepted that harmonics with an intensity of less than about 20% of the magnitude of the harmonic of greatest intensity contribute insignificantly to the tone. I'd like to extrapolate this to point out that absence of harmonic frequencies can also significantly color tone. In addition, a plucked string differs significantly from a struck string. A struck string favors formation of higher partials because all partials have (in an ideal model) a potential for the same intensity. The plucked string, however, favors partials inversely to the square of their ordinal number: the fundamental has a potential of 1, the octave has a potential of 1/4, the second harmonic has a potential of 1/9, etc. While these facts contrast a piano string versus a guitar string, they can be significant for bassists who play certain styles. Percussive string attack is an increasingly common stylistic approach for guitar as well.

Another "law" applying to the formation of harmonics of the vibrating string is that the first six partials are generally agreed to be harmonious. We can add the eighth, tenth, twelfth, fifteenth, and sixteenth without impairing the consonance of the tone. Due to natural string division, the seventh, eleventh, thirteenth, and fourteenth are discordant. They are mathematical multiples, but they do not belong to the musical scale; therefore they impair the consonance of the tone.

One final point concerning the plucked string is that the picking point can suppress the formation of harmonics. Guitarists avail themselves of this principle all the time. Strumming or picking closer to the bridge suppresses the lower partials and makes the tone brighter. Strumming or picking closer to the neck suppresses the higher partials and sounds fuller and warmer. The picking point in these tests was carefully controlled to be at an exact fraction of the string length, rather than a consistent distance from the bridge.

Spectrum Comparisons

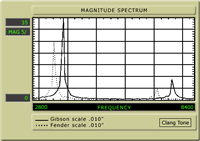
Now, let's view some of these spectrum analyses in greater detail. The first three (Fig. 2, 3, and 4) will compare a .010 gauge string tuned to 330Hz, a high E on the guitar, at three common scale lengths. I'll also state for the record that we did literally dozens of tests to ensure that we got consistent results. Let's look at the 25 1/2" scale (Fig. 3) The strongest component, the first four partials, are fairly smooth (up to 1320Hz). The fifth, ninth, and thirteenth contribute significantly, about 30% to 40% intensity (that's 1650Hz, 1980Hz, and 4290Hz). Remember that the thirteenth sounds discordant, and note that we see almost no activity at the seventh and eighth, and tenth and eleventh. There's a big "valley" between 2200Hz and 2800Hz—very interesting—an absence of a wide band in the upper midrange.

Fig. 3

Fig. 4

Let's compare this to the 25" scale (Fig 4). The strongest component, the first four partials, are not very smooth. The first harmonic, the octave, is about 20% stronger than the others. We're also getting a significant contribution from the fifth, ninth, tenth, and twelfth, (1650Hz, 2970Hz, 3300Hz, and 3960Hz), at about 36% intensity, and the sixth, eleventh, and thirteenth are also contributing at about 25%. Note that the eleventh and thirteenth are discordant, and again there is a little activity at the seventh and eighth. This may be explained by the plucking point that I chose: 1/8 of the scale length, approximately where a guitarist would commonly pluck.

If we examine the 24 5/8" scale in Fig. 2 (7/8" shorter than the 25 1/2" scale) we see that the first four partials are also not smooth, rather like the 25" scale with a strong second (octave) harmonic. We can also see that the higher partials contribute little to the tone, as the fifth is about 25% and the ninth is at about 30%, and all others are insignificant. There isn't much top end "sizzle" in the shorter scale length. None of this should be surprising to seasoned builders and players. These tests bear out what our ears tell us. We can conclude that the 25 1/2 " scale offers the "smoothest" harmonic response with good presence of the first six partials (the most harmonious), and a bit of the thirteenth for "character" or "edginess." The 25" scale has a less smooth harmonic content with a bit more upper mids. It's also fairly strong in the number of discordant partials (eleventh and thirteenth). The 24 5/8 " scale has the strongest character in the first four partials, with relatively little above the first four. There is an absence of discordant partials, possibly because the shorter length and decreased tension won't allow the string to divide easily into higher partials.

Fig. 5 shows the spectrum analysis of a wound string, a .024 gauge nickel wound, tuned to G at 196Hz. We'll compare the 24 5/8" " scale (shown in black) and the 25 1/2" scale (shown in grey). Both scales exhibit strong first octave components, with the fundamental, third, and fourth partials about equal, but only about 60% of the strength of the second partial. The fifth partial (two octaves plus a third), is relatively strong at between 40% and 60% of the octave, and the ninth and tenth partials between 20% and 25% the strength of the octave. There's a "scoop" between 1100Hz and 1700Hz an absence of upper midrange. Although texts claim that harmonics with less than 20% contribution are tonally insignificant, I find it interesting that there is almost no activity at the sixth harmonic, 1372Hz, for the longer 25 1/2 " scale, while the shorter scale shows twice the activity (still tonally insignificant?).

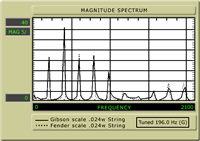
Fig. 5

The 25 1/2 " scale, represented by the grey line, has a minutely (about 10%) stronger third partial, the fifth partial is about 14% stronger, and the eighth and ninth partials are again about 33% stronger than the 24 5/8" scale, but still only about 25% of the second partial. The slight increase in upper partial intensity of the 25 1/2" scale is not as dramatic as we saw with the plain string, but it is evident, with 2, 4, 5, 8, and 9 stronger for 25 1/2 These tests graphically demonstrate, to some extent, what we intuitively know about scale length and the harmonic voices of the scales.

Clang Tone

Something that has me particularly excited is the "clang tone" concept. The clang tone is the result of the elasticity of the vibrating string. It is the tone of the string stretching and relaxing as it performs its transverse vibrations, and is referred to as longitudinal vibration.

A taut string actually vibrates in three modes: transverse, which we are most concerned with; longitudinal, which is usually the concern of piano builders because the struck string has greater potential for excitation of higher harmonics; and torsional, or twisting of the string, which has no musical value, only mathematical value.

Some interesting points about the clang tone:

• It is almost completely unaffected by tension! Altering the tuning of the string by changing the tension does not change the clang tone by more than a "comma" over the entire range of tension of the string.
• It is minimally affected by mass or weight.
• It is primarily affected by length.

Where does the clang tone "live?" One source states that in a piano it can be found at about three octaves and a fifth to about four octaves and a third above the fundamental. Another source says that it is at least ten times the frequency of the fundamental.

I'd like to demonstrate a clang tone for you. I have a guitar, some rosin, and a rag. First, we'll produce the tone with the string tuned to pitch. I'll rub some rosin on the rag and glide it along the string. EEEEK! Sounds like someone learning to play the violin! Now I'll lower the tension of the string and compare the clang tone. EEEEK! Sounds the same, doesn't it? Just to be sure, I'll tune it up again. EEEEK! That's a horrible sound, but it's amazing that the pitch doesn't change when the string is re-tensioned. 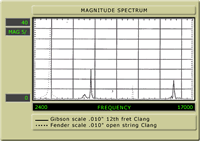We can view the clang tone in Fig. 6 and spare our hearing. This is a.010 string, tuned to E at 330Hz at the 24 5/8" scale (black) and the 25 1/2 " scale (grey). We find the clang for the 24 5/8" scale at 3850Hz, and the clang for the 25 1/2" scale at 3500Hz. It definitely changes with the scale length. Just to show the consistent relationship, we also tested for the clang tone at the octave (Fig. 7). The 24 5/8" scale clang shows clearly at 3850Hz and the octave (twelfth fret, or 12 5/16" clang at 7700Hz. The magnitude of the octave clang is, coincidentally, about half the magnitude of the full scale clang, and a bit stronger than the octaves of the full scale clang.

Fig. 6

Fig. 7

Review

• We must consider scale length when we are building to satisfy a tonal parameter. The scale length we choose may dictate certain other parameters of our construction, so we must consider scale length first.
• The voice of the scale length will determine the harmonic "input" that the woods and electronics will have available to filter, resulting in the sound of the completed instrument.
• Since all parts of the instrument interact act upon the other parts as they themselves are acted upon we can't quantify the relationship of scale length to the other parameters of instrument construction. We can, however, form an "intuitive familiarity" with how scale length affects the tone of our completed instruments.
• The scale length voice is clearly made up of peaks of harmonic intensity that will vary with the length chosen. Remember that the lack of intensity at particular peaks also colors the voice of a particular scale.

Audience Questions

Audience: I'd like to know if the patterns you showed us were mathematically developed or measured in an actual sound environment.

Using the monochord I described earlier, we carefully controlled the string tension and length, as well as picking point and pressure. We did dozens of tests, discarding ones that had serious problems, and Bill's watchful analytical eye was always looking for inconsistencies and artifacts. The ones you're seeing here tonight are repeatable and representative of the total samples.

I also have many more questions myself If this equipment were at my disposal to use at any time I'd explore the clang phase relationships in detail, especially as notes are fretted, and compare the various scale lengths. This may account for Marc Silber's comment to the 1992 GAL Convention that "some scales just don't tune" which from a purely Pythagorean point of view seems improbable, but in practice may point up problematic clang phase relationships with certain scale lengths. Does compensation in the individual strings of a single scale length guitar introduce clang phase relationship problems or beat frequencies? This is another question that needs further investigation.

Audience: What is your time frame?

Since this is a spectrum analysis and not a wave form, the sample is limited to a fraction of a second immediately after the pluck, when the harmonics are richest, and the vibrations have stabilized.

Audience: Earlier, you produced the clang tone on a string that was already up to tension. How about a slack string?

We can try that right here. The clang tone changes almost imperceptibly with tension, but since we're discussing vibrating strings, we will need a little bit of tension. By the way, from what I've read, the string is most elastic up to 70% of its breaking strength. When that 70% point is exceeded, the string loses elasticity rapidly. There. Is that loose enough? (String sounds "boinnggg. " Audience agrees it is loose enough.) I'll put a bit of rosin on the cloth and... EEEEK! Now I'll tune it back up arbitrarily (string sounds "twanngg") and rub it... EEEEK! Sound like the same pitch? (audience agrees) I think we don't want to build a lot of that into our sound!

Audience: When you compared the short and long scales, did you try keeping the tension the same and testing both scales?

As we remember from Mersenne, that would result in different pitches, so the harmonic peaks wouldn't align. If we tested at 196Hz and 188Hz, how could we compare the harmonics? Perhaps we could vary the weight of the string to maintain tension at different scale lengths, but that also changes the way the string vibrates because it changes its elasticity, so we'd be comparing apples to oranges.

Audience: When you finger a chord, aren't you creating a number of different scale lengths?

Yes, that's exactly what you're doing. You're fingering a chord, which will have its own pattern, based on the contributing tones; the scale length vs. string size vs. tuning relationships for each note of that chord. So, while the concept of scale length may seem nebulous when applied to the complexities of actually playing the guitar, we can see that when broken down to the individual string tone, it is vital in determining that tone, and a particular scale length will color the tone of chords built from notes generated by that scale length. These graphs can only show us that a relationship exists. The exact parameters for our instruments will vary, but I believe that the general relationships will remain consistent. It is my hope that this information will broaden your understanding of guitar making, will be useful to you immediately, and may help you to achieve something elusive that you've been seeking.